CATEGORIES FOR ARTICLE LINKS BELOW

Fact or fiction? Tire contact patch size is determined mostly by weight and tire pressure.

Written By: http://performancesimulations.com

Heard this before? "Only air pressure and weight (tire load) dictate contact patch size. Tire width has nothing to do with it. If you double the width of a tire you cut the length of the contact patch in half. You get the same contact patch **area** either way. This is described by the following equation reasonably accurately (maybe within a 5-10% error range?):

tire_pressure = weight / contact_patch_area

Therefore: contact_patch_area = weight / tire_pressure

Basically there are two camps on this one among people not actually in the field:

A) It's true.

B) It's false.

Shocked? I didn't think so. Which is it though? I wish I was good enough with web design to force you to vote at this point before continuing, just out of my own curiosity. Quite frankly, I wasn't entirely sure. I had measured contact patch sizes under varying loads for little, almost solid, foam rubber RC tires during development of a theoretical tire model for vehicle simulation, where the contact patch didn't grow nearly in scale with the changes in vertical force, but those are little foam rubber tires. No air. A balloon indeed will follow the above equations. I always figured a full sized, pneumatic (air filled) tire would fall somewhere in between the two extremes. But towards which side and how far?

Let's take a look at some real life data measured from real tires on a real flat plate under controlled circumstances by a tire manufacturer. Avon tires was gracious enough to post extensive data on many of their tires at their web site (including Pacejka Magic Tire Model constants for you other car sim developers out there!) What follows is an analysis of that data for one pair of tires with the purpose of shedding some light on this subject. This was done as a simple curiosity, but I was surprised enough at the results to share them here as they appear quite revealing.

Avon had a simple test we all probably have imagined at one time or another, but never had the means to do it. They pressed their F3000 racing tires (among others) against a flat plate that simulates the ground. By increasing force and measuring the amount of tire deflection, or more specifically, the change in radius or the distance from the centerline of the tire to the ground, they are able to illustrate and give engineers several useful pieces of information. They weren't specifically measuring contact patch size, but we can get an accurate enough estimation of contact patch size versus load and contact patch pressure from the data to see something quite revealing.

We are looking at data for the following tires:

(Rear tire?): Avon F3000 315/660R13 with 651.5mm diameter on 13.75 inch rim. Readings taken from a flat plate.

(Front tire?): Avon F3000 245/635R13 with

The tire diameters are within 1.6% of each other.The rear is 28.5% wider than the front. Now, don't get excited, we're not going to look at grip or tire force curves here, so we don't need to even try to talk about tire compounds. One point Camp A argues is that the wider tires have better cooling, so a wider tire typically is made of a softer compound and that's the reason it gets more grip. I.e., it's not because they have a bigger contact patch. Fine. But if the contact patch is not really the same size (within a reasonable tolerance of course) than the argument is based on something bogus (even if the wider tires DO have softer or better gripping compound. I've never built a tire or talked with a tire engineer so can't be 100% certain.) Wider tires probably do have better cooling since a given tread element spends less of its travel time around the tire within the contact patch. This is all sideshow talk and misses the real root of the argument though. In this exercise all I wanted to explore were answers to the two questions below. Most arguments I've read either way stem from a disagreement on the answers to these two questions:

1) "Does a significantly wider tire of similar diameter, possibly similar construction, essentially identical application, built/designed by the same manufacturer for the same car and use, have essentially the same contact patch size at a given load and pressure as it's narrower counterpart?"

2) "Does the contact patch size of a tire REALLY scale with the vertical load? I.e., if you double the load (weight), does the contact patch size double? After all, it must if the area = weight/tire pressure equation is right."

Granted, I haven't seem anyone claim they will be exactly the same. Generally people seem to agree that these statements might be accurate to maybe 90%-95% of reality. I also believed and stated this very same thing online several times. I'm ashamed of having done so without looking at any data, however! Ok, as stated already, Avon did not measure the contact patch size directly. However, it is probably accurate enough for our purposes to calculate the contact patch size by imagining the tire is a cylinder and penetrates the ground plane by the same depth as the vertical deflection that was measured on the tire tester. Agree? After all, any part of tire a that would be "underground" must be squashed against the ground and be part of the contact patch. Is this model 100% accurate? No, of course not, but it's probably within the same 5-10% error that we're assuming in the statements we're examining, so let's try that assumption and see where it takes us. If we find we're within maybe 10% or so, then the tire data doesn't really prove anything for either camp. But you never know for sure until you do a test!

Avon did their tests at four different tire pressures for both tires: 28psi, 24psi, 22psi, and 18psi. By calculating the contact patch area with the above assumptions, we should then be able to calculate average pressure in the contact patch since we know the vertical force. Remember, if Contact_patch_area = Weight / Tire_pressure then the average contact patch pressure we calculate should be reasonably close to the actual tire pressure and not change a whole lot throughout the load range. I.e., Camp A says that if you double the weight on the tire the contact patch pressure remains the same. The contact patch simply doubles in size by becoming twice as long. If you double the width then you also keep the same area (since contact patch pressure must remain approximately constant). Instead of increasing patch size you simply change its shape. It's twice as wide and half as long.

What we assume below are in a sense, perfectly rigid sidewalls along the lateral (tire width) direction.. I.e., the tire is pressed down and the chord across the circle that represents the tire/ground intersection gives the contact patch length. In reality, the sidewalls deflect outwards somewhat, so it makes sense that the actual, real contact patch length will not grow as quickly as it does in the tables below. The assumption that the sidewalls can not flex laterally skews this data more in favor of Camp A's arguments since it will cause the contact patch length (and therefore area) to grow more rapidly than it would in reality with increasing load, but as you'll find out, this tidbit merely backs up Camp B's argument even further. Here are the calculations made:

Half_Patch_Length = SQR(Tire(0).Radius * Tire(0).Radius - Tire(i).Radius * Tire(i).Radius)

Patch_Length = 2 * Half_Patch_Length Patch_Area = Patch_Width * Patch_Length

Patch_Area = Patch_Area * 0.0015500031 Tire_Load_LB = Tire(i).Load * 2.20462262

Contact_Patch_Pressure = Tire_Load_LB / Patch_Area SQR(----) means "the square root of" * means multiply / means divide

There is some converting in there because I wanted to show the patch area in square inches instead of square millimeters (multipication by 0.0015500031) and I wanted the tire load to be in pounds instead of Kg as was provided (multiplication by 2.20462262). This way we can compare PSI air pressure to PSI contact patch pressure. Tire(0).Radius is the undeflected tire radius. Tire(i).Radius is the tire radius at whatever tire load is listed in that row. The difference between the two (not shown) is the tire deflection. These pieces of information are the actual, measured data supplied by Avon. The contact patch length, area, and pressure are calculated per the above equations. Remember that with the equations above, the tire structure is effectively constrained in a way that forces the contact patch size to grow more than it would in reality with increasing load.

Since the real contact patch size would likely increase more slowly than it does in the tables, the real patch pressure probably increases more rapidly than what we see here. Remember, the foundation of Camp A's argument is that contact patch pressure should remain pretty close to constant and equal to the tire's air pressure.

In essence, these tables are likely a rather conservative view and understate the dramatic change in contact patch pressure, further indicating that contact patch pressure is not very well tied to air pressure at all. Front Avon F3000 tire -- unloaded tire radius of 320.8 mm.

28 PSI

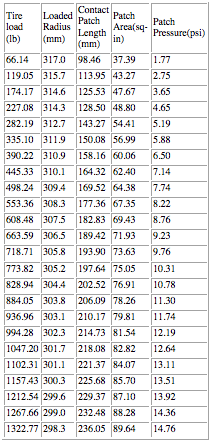
I had a difficult time believing what I was seeing when looking at this data. According to the Avon data and these calculations, the contact patch pressure not only does not remain close to constant, it never even approaches that of the air pressure in the tire. Granted, sidewall deflection is not included here so in reality the contact patch pressures are likely to be higher than what is shown, possibly significantly. But what is immediately obvious is that doubling the load does not double the contact patch area. I.e., the contact patch pressure does not remain constant.

From 390 lb to 773lb (almost double the tire load) the contact patch size only increases by 25%, even assuming laterally constrained sidewalls! Additionally, the calculated contact patch pressure rises from 6.50psi to 10.30psi, a whopping 58% increase in patch pressure. And again, since it is likely that the contact patch size grows even more slowly than what the tables show due to sidewall deflection, the contact patch pressure likely increases even more rapidly than what we see here.

The point here is, even if the calculated contact patch data was wrong, the trend is still obviously in the direction that contact patch pressure and air pressure are not very intimately related at all. I.e., the equation

Camp A uses: contact_patch_area = weight / tire_pressure

....is not even close. Those contact patch pressures should be pretty close to constant and somewhat in the tire pressure's ballpark throughout the load range if the equation is really a reasonable approximation of reality.

Let's move on to the rear Avon F3000 tire so we can see a similar tire that's 28% wider. What do you guess will happen to the contact patch size? I expected to see it be larger, even at typical loads: Rear Avon F3000 tire -- loaded tire radius of 320.8 mm.

28 PSI

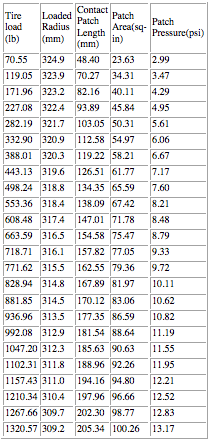
Again, I was surprised. If we look in the middle range at a load of 553 lb, the calculated contact patch area is 67.42mm. At the same time, the front tire at almost the same load has a contact patch area of 67.35mm. This is almost no change at all, and in fact within a reasonable error limit it is probably sufficiently accurate to say that the wider tire has the same contact patch area as the narrower one does at around 500 lb load. At very low and very high loads the wider tire does have a larger contact patch size, however. It appears to be only in the middle range that the pressure and patch size are very similar, even though this tire is 28% wider than the first one. Note, however, that at 1320 lb load the rear has a patch size of 100.26 and the front is only 89.64, an 11% difference. One might guess that Avon intentionally designed the tires this way. Regardless, I believe this data shows that things are not quite so simple with tires as patch_size = weight / tire_pressure.

So does widening the tire cause a bigger contact patch? Well, over most of the load range for this particular tire it does if they can be compared directly this way, but the contact patch size does not increase by the same amount as the width of the tire (28% vs. 11% at the greatest load). At the same time, under more typical loads the contact patch sizes are quite similar.

However, this at a high, 28 PSI tire pressure. Something I was not expecting happened when they started lowering the air pressure in both tires.

Before looking at that, let's see the rest of the front tire data for the other air pressures that were tested: Front Avon F3000 tire -- unloaded tire radius of 320.8 mm.

24 PSI

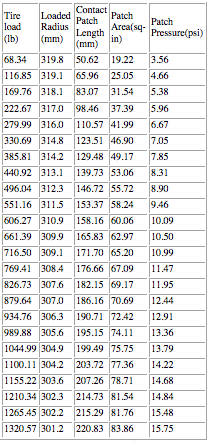
This data is the most puzzling of all and can be compared with the first table on this page. What is interesting here is that even though the air pressure was lowered, the amount of vertical tire deflection actually decreased at many loads. At 28 psi and 553 lb load the tire radius was 308.3mm versus the 24 psi tire radius of 311.5mm. The calculated contact patch size actually decreased from 67.35 square inches to 58.24 square inches. I don't understand it, but there it is:. They took 4 psi out of the tire and it had less vertical deflection at 550 lb load! It looks like tires are little more complex than balloons after all. The physical tire structure and construction obviously can not be ignored or assumed to be "only 5-10% of the picture."

22 PSI

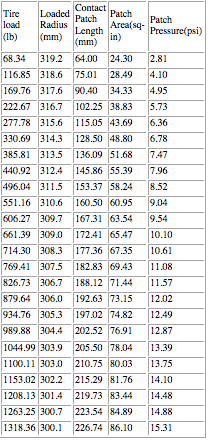
18 PSI

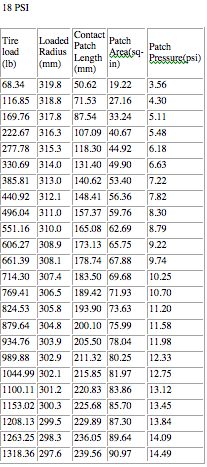
Through the last two tables things are basically as expected. As air is removed from the tire the deflection at each load is greater and the contact patch grows. The 24 psi data is bizarre, but the general trend over all four tables is as most people would expect. Drain out the air and the tire center sits lower (past ~24 psi anyway). However, note that the deflection and calculated contact patch area/pressure don't change nearly as much as tire pressure would indicate if contact_patch_area = weight / contact_patch_pressure gave a reasonably accurate picture of reality. At 550 lb load, lowering the air pressure from 28 psi to 18 psi should increase contact patch size by roughly 55% if that formula is even close to reality.

Now is that bizarre or what? The 18 psi tire actually had LESS vertical deflection than the 28 psi tire did at 550 lb load. Remember, the vertical deflection and force (first two columns) are actual measured, Avon test data, and are not subject to any calculations on my end at all so they can't possibly be "wrong." That data can be verified at Avon's web site. The remaining columns are calculated, however, but make sense in light of the strange, unexpected changes in vertical deflection observed here. Strangely enough, at 18 psi the contact patch size on this tire appears to be smaller than it was at 28 psi, and the contact patch pressure increased only very slightly, by about 7% rather than 55% as would be expected.

The 18 psi tire sits higher at these two loads than the 28 psi one does! There's less vertical deflection. That's an Avon fact. I don't pretend to understand why this is so, but there it is. And again, when they doubled the load the calculated contact patch pressure does not double along with it, regardless of the tire pressure. It increased by 53% (high pressure) and 41% (low pressure) respectively.

When lowering the narrow tire's air pressure from 24 psi to 22 psi, the contact patch size grows 4%, not 9%. And don't forget about our constrained sidewalls! In reality the patch will grow even less than this. What else is interesting is that at this load, the wide tire's contact area increases by the same percentage as the narrower one does as pressure is reduced from 24 psi through 18 psi. I suspect that the constrained sidewall assumption skews the data in a way that means that the real wide tire grows its contact patch more rapidly than the narrow one. How much so is not known.

Contact patch pressure is constant and equal to air pressure? No, not even close. Wide tires have a greater contact area? From this data it appears very likely. Which would mean the "wide tires are softer and therefore give more grip" argument is bunk. The contact patch is bigger, and the contact patch pressure is lower. Avon has several sets of tire data available. Feel free to do your own analysis on any of the other tires. It appears likely from looking at this data is that if lateral sidewall deflection were included, the contact patch size might change by a rather small amount when the load is doubled in a typical operating range. The contact patch certainly does NOT get twice as long and the contact patch size certainly doesn't double. The above tables show the absolute limit to how much the length and areas could increase. In reality the changes must be even less.

ATTENTION READER:

If you enjoyed the information and article you just read be sure to check out our newly released book with even more exciting photo's and information:
How to Turbocharge and Tune your Engine

Follow Enginebasics on...

Want to know more about your particular Make and Model vehicle? All of these vehicles are covered in the tech, maintenance and repair articles found above. Enginebasics is the wiki or wikipedia of car part, repair, how to and tuning information. Let us be the class 101 for your automotive learning.

Individual Models

Below are just a few of the articles found here on enginebasics.com

Reading Spark Plugs	Camshaft Understanding	Engine Timing	Intake Runner Length	Exhaust Flow Tuning	Camshaft Timing	Engine Cooling Basics	Compression Testing	Forced Induction
Tuning A/F Ratio Basics	Intake Manifold Basics	A look at cooling mods	Camber Caster Basics	Sequential Vs Batch Injection	Fuel Pressure Regulator	EGT Vs A/F EFI Tuning	Engine Start Programming	What is a fuel Injector?
Brush vs Brushless Motors	4-stroke motor diagram	Crankshafts Basics	Automotive Relays	EFI Tuning Basic Thoery Guide	Understanding Electric Motors	Water Meth Injection	Intercooler Basics	e85 Basics
Water to Air Intercooling	Turbo Surge	EFI Air Intake Temp Tuning	Map vs. MAF Sensor EFI Tuning	Engine Start up tuning for EFI Cars	Building an EFI Surge Tank	Intercooler Efficency	Boost Controllers	Engine Oil Weights
Exhaust Cutout Basics	Cold Air Intake vs Short Ram	Engine HP and Torque Basics	Intercooler Sprayer Basics	Turbo Manifold Design Basics	Cryo Liquid Co2 Cooling	Oil Cooler Basics and Installation	Boost by Gear Tuning	Closed Loop vs Open Loop O2 tuning
Changing your own oil	Static Vs. Dynamic Compression	Air to Air Vs. Water to Air Intercoolers	Vented vs Recirculating Blow Off Valves	Engine Intake Exhaust Valves	Wiring a fuel pump relay	Synthetic vs Regular Oil	O2 Sensor Repair Fix	Embrace the TURBO LAG

**TO SUBMIT AN ARTICLE TO ENGINE BASICS PLEASE CLICK: CONTACT US!

Testimonials Page

“Thank you, for the info, on your site, on how to remove valve springs, and install stem seals, using normal shop tools. Info from every other site I looked at, only said how to do it using costly special tools. Thank you for showing the REAL easy way, and saving me some money.”   Joe S

“Hello there,
            Don’t have any questions, just wanted to say thanks for putting this info out there.  So much mis-information on forums, good to read some solid info. Peace” Jay R.

Privacy policy and terms of service

Advertise

Copyright 2010 EngineBasics.com: Engine Basics. All Rights Reserved

Enginebasics Google+ Page